用 Swift 写算法——递归和分治法 分治法简介 将问题分解,通过求解局部性的小问题来解决原本的问题,这种技巧叫分治法。实现分治法需要使用递归,其主要步骤如下:
将问题分割成局部问题 (Divide)
递归地求解局部问题 (Slove)
将局部问题的解整合,解决原问题 (Conquer)
应用-穷举搜索 题目:
现有数列 A 和 整数 m。请编写一程序,判断 A 中任意几个元素相加是否能得到 m。A 中每个数只能用一次。
Swift 实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 let array = [1 ,5 ,7 ,10 ,21 ]func solve (i : Int , m : Int ) -> Bool { if m == 0 { return true } if i >= array.count { return false } let res = solve(i: i + 1 , m: m) || solve(i: i + 1 , m: m - array[i]) return res } solve(i: 0 , m: 8 )
分析:
我们把问题分解成两个更小的局部问题:选择当前元素/不选择当前元素的情况下搜索。如此递归下去,便能解决原问题。
检查所有排列组合需要使用两个递归函数,时间复杂度为 $O(2^n)$ ,因此 n 不能太大。
应用-科赫曲线 题目:
编写一程序,输入整数 n,输出科赫曲线的顶点坐标。
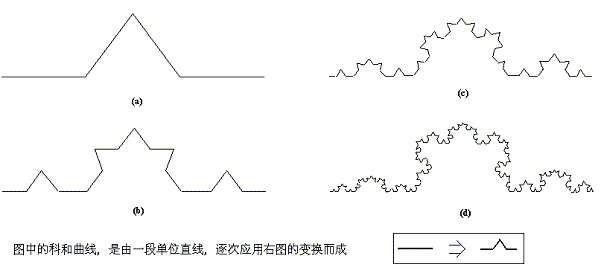
科赫曲线是一种广为人知的不规则碎片形。该图形具有递归结构,可以通过如下方法画出:
给定线段三等分
以三等分点作出正三角形
对新产生的线段重复上述操作
设端点为(0,0)和(100,0)
Swift 实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 func koch (deep :Int , a :(Double , Double ), b :(Double , Double )) { if deep == 0 { return } let left = ((b.0 - a.0 )/3.0 + a.0, (b.1 - a.1)/ 3.0 + a.1 ) let right = ((a.0 + 2.0 * b.0 )/3.0, (a.1 + 2.0*b.1)/ 3.0 ) let mid = ((right.0 - left.0 )* cos(1.0 /3.0*Double.pi) - (right.1 - left.1)*sin(1.0/ 3.0 * Double .pi) + left.0 , (right.0 - left.0 )* sin(1.0 /3.0*Double.pi) - (right.1 - left.1)*cos(1.0/ 3.0 * Double .pi) + left.1 ) koch(deep: deep - 1 , a: a, b: left) print (left) koch(deep: deep - 1 , a: left, b: mid) print (mid) koch(deep: deep - 1 , a: mid, b: right) print (right) koch(deep: deep - 1 , a: right, b: b) } koch(deep: 2 , a: (0 ,0 ), b: (100 ,0 ))
分析:
每次都计算出左、中、右三个点的坐标,然后逐层递归。把最原始的问题化成端点到左,左到中,中到右,右到端点这些规模较小的子问题,同时,递归层级递减,直到 0。