Backpropagation and Computational Graphs

我在大四的时候上过一门课叫 Computational Intelligence，当时有一次作业就是写一个简单的神经网络。遗憾的是当时并不了解向量化的含义，对反向传播的理解也只局限于每个神经元怎么更新自己的权重。可想而知，当时我写的是一个很不优雅、运行效率很低的程序。现在试着从另一个视角来理解神经网络和反向传播算法。

Neural Networks

一般我们理解的神经网络都是如下的结构：

一个个神经元互相连接，非常直观，也很像我们大脑中神经网络的样子。但其实完全可以用纯数学的方式（不掺杂一点生物学概念）来理解神经网络。它其实就是一个线性分类器，经过一个非线性函数后，再输入给下一个线性分类器…… 中间的非线性函数是必不可少的，否则整个神经网络就将塌缩成一个大的线性分类器。

普通的线性分类器可以表示为：
$$
s = W\cdot x
$$
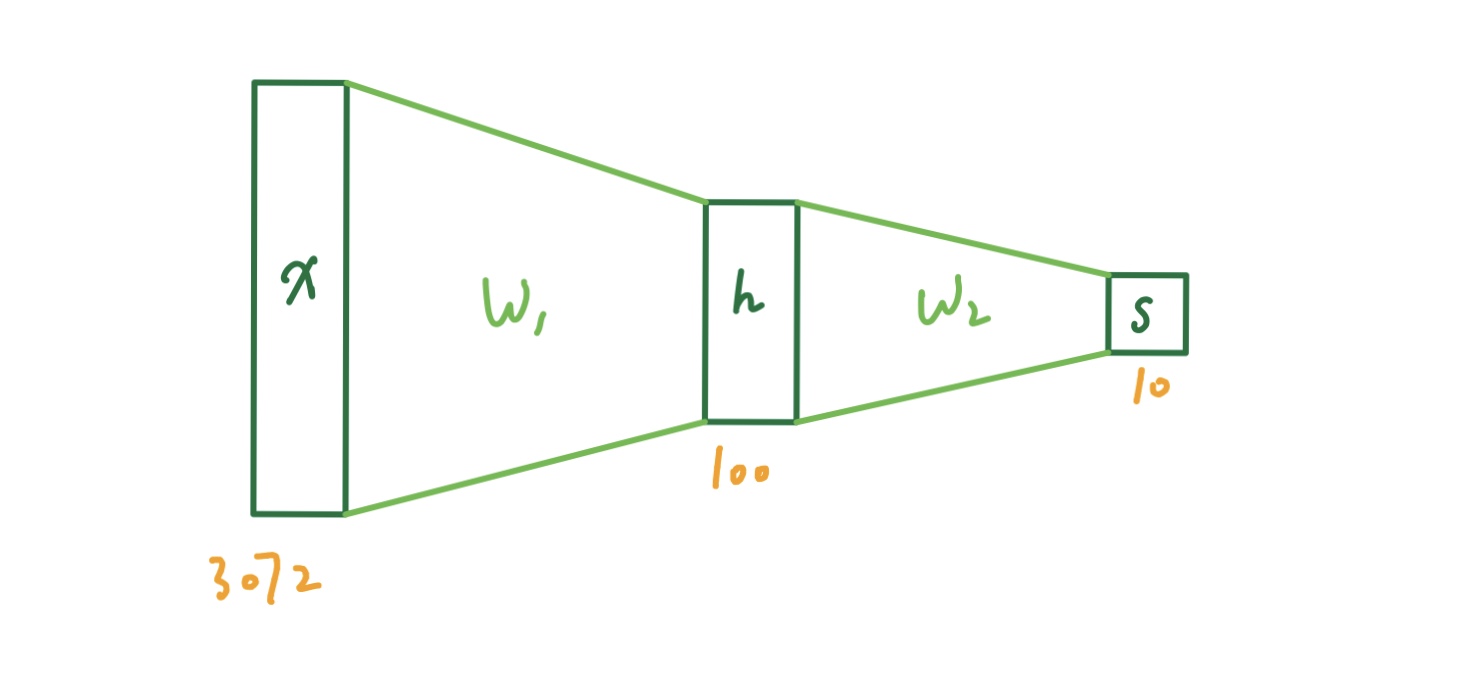
其中 x 是输入，如果是一个 32x32x3 的图像的话，就可以表示为（3072, 1）的列向量。W 作为参数为（10, 3072）的矩阵。这样相乘得到一个十个元素的向量，对应 10 个不同分类的得分。

那么一个两层的神经网络就可以表示成：
$$
s = W_2max(0,\space W_1 x)
$$
其中的 max 就是上述的非线性函数，被称为 ReLU（Rectified Linear Unit）。当然我们还有很多很多其他的非线形函数可以选择，比如 tanh 或者 Sigmoid 函数。这个函数也就是所谓的激活函数（activation function）。这样的神经网络看起来就像下图的样子。

类似地，三层的神经网络可以表示为：
$$
s = W_3max(0,\space W_2max(0, \space W_1 x))
$$
W1, W2, W3 也就是我们要通过 SGD（Stochastic Gradient Descent）学习的参数。

Cross-Entropy Loss (Softmax)

为了优化参数，我们需要定义一个损失函数（Loss Function）。我们仍然可以使用 Softmax 分类器的交叉熵损失函数。交叉熵把输出的 score 看作是概率。
$$
L_i = -log(\frac{e^{f_{yi}}}{\Sigma_je^{f_j}})
$$
log 里面的部分即为 softmax 函数。这个函数把一个普通的向量中的元素都压缩到 0 至 1 的范围内，并让他们相加得 1，这样就可以用概率来解释了。

上面的公式等价于：
$$
L_i = -f_{y_i} + log\Sigma_je^{f_j}
$$
Softmax 分类器既可以用概率论的视角也可以用信息论的视角来解读。这里我们只关心这个损失函数。

我们可以写出计算 loss 的 numpy 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def loss(self, X, y=None, reg=0.0):
  W1, b1 = self.params['W1'], self.params['b1']
  W2, b2 = self.params['W2'], self.params['b2']
  N, D = X.shape
      
  scores = None
  loss = None
      
  out1 = np.maximum(0, X.dot(W1) + b1) # relu, (N, H)
  scores = out1.dot(W2) + b2 # (N, C)
        
  correct_class_score = scores[np.arange(N), y].reshape(N, 1)
  exp_sum = np.sum(np.exp(scores), axis=1).reshape(N, 1)
  loss = np.sum(np.log(exp_sum) - correct_class_score)
  loss /= N
  loss += 0.5 * reg * np.sum(W1 * W1)+  0.5 * reg * np.sum(W2 * W2)

注意最后还要加上正则项（这里用的 L2 正则），它可以让模型的参数尽量简化。

Computational Graph of NN

计算图可以用来表示任意的数学表达式。它可以自动微分的特性使得主流的深度学习框架都以计算图为核心。一个两层的神经网络可以画成：

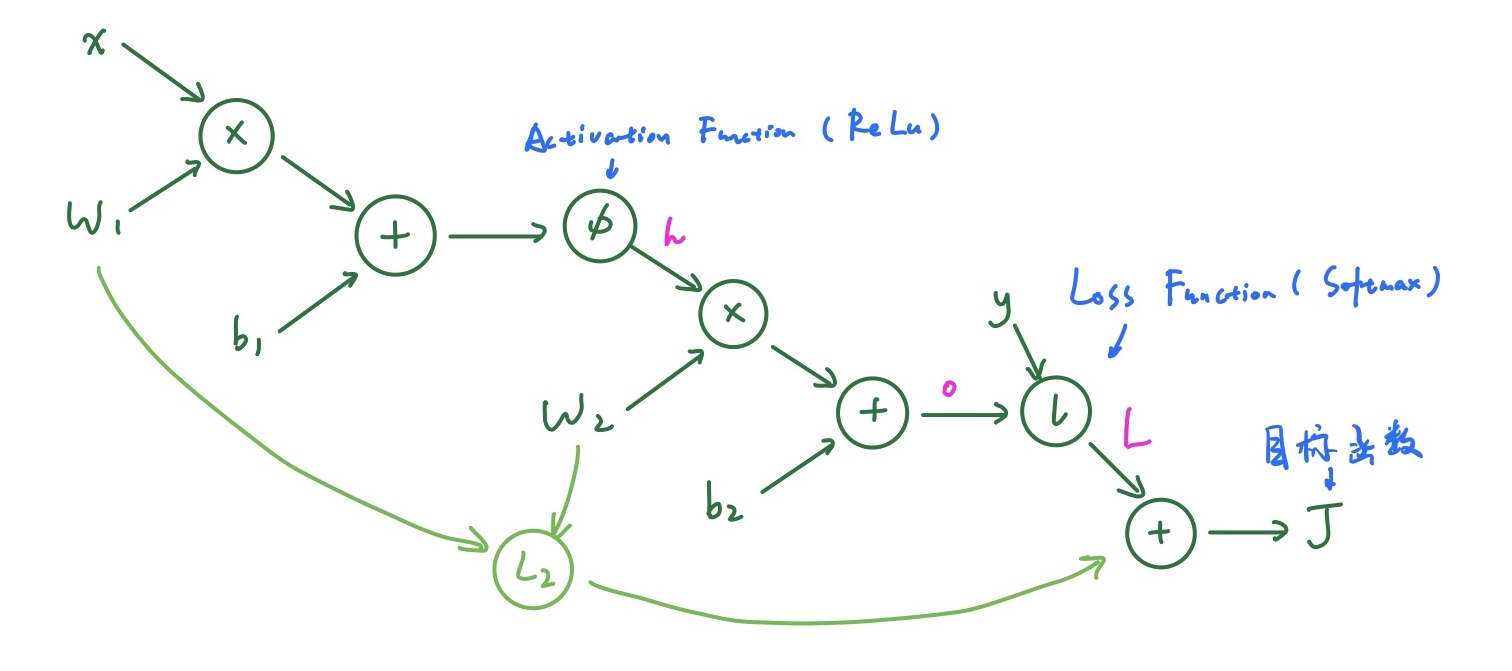
Backpropagation

我们需要 loss 和 gradient 才能使用 SGD 来学习参数。通过正向传播，很容易计算出 loss，而 gradient 就要通过反向传播来计算。

即我们要求出以下四个导数的值：
$$
\frac{\partial J}{\partial W_1},\space \frac{\partial J}{\partial W_2},\space \frac{\partial J}{\partial b_1},\space \frac{\partial J}{\partial b_2},\space
$$
从后向前计算：
$$
\frac{\partial J}{\partial L} = 1 \
\frac{\partial J}{\partial o} = \frac{\partial J}{\partial L} \cdot \frac{\partial L}{\partial o} = \frac{\partial L}{\partial o}
$$
Recall Softmax 函数：
$$
L_i = -o_{y_i} + log\Sigma_je^{o_j}
$$
可以看到这里有两项 o，因此分开算：
$$
\frac{\partial L_i}{\partial o_{y_i}} = -1 \
\frac{\partial L_i}{\partial o_{j}} = \frac{\partial log\Sigma_je^{o_j}}{\partial o_{j}}=\frac{e^{o_j}}{\Sigma e^{o_j}}
$$
继续对 W2 求导可得：
$$
\frac{\partial J}{\partial W_2} = \frac{\partial J}{\partial o}\cdot h + \lambda W_2
$$
我们可以写出对应的代码：

1
2
3
4
5
6
7

margin = np.exp(scores) / exp_sum
margin[np.arange(N), y] += -1
margin /= N #(N, C)
dW2 = out1.T.dot(margin) #(H ,C)
dW2 += reg * W2 
grads['W2'] = dW2
grads['b2'] = np.sum(margin, axis = 0)

类似地，求解 W1 和 b1 的导数代码为：

1
2
3
4
5
6

margin1 = margin.dot(W2.T) #(N, H)
margin1[out1 <= 0] = 0 # 正向传播时 ReLu 过滤掉了一部分，这部分实际上对 loss 是没有任何贡献的。因此反向计算时也要把这部分排除
dW1 = X.T.dot(margin1) #(D, H)
dW1 += reg * W1 
grads['W1'] = dW1
grads['b1'] = np.sum(margin1, axis = 0)

可以看到，我们在正向计算时缓存了一些中间变量，而反向计算时就可以直接使用了，这有一些动态规划的意思。而且整个计算时全向量化的，没有嵌套循环。Numpy 底层使用 C 编写，本身循环速度会比 python 快很多，再加上许多优化处理，例如优化缓存命中率或利用 CPU 的 SIMD 指令等，因此非常高效。向量化得代码还有助于后续在 GPU 上加速计算。