Forward & Backward Pass of Batch Normalization
原论文地址:https://arxiv.org/pdf/1502.03167.pdf
标准化过后的数据更利于机器学习。在神经网络中,数据分布不均匀的情况不仅仅会发生在输入的原始数据中,也会发生在隐含层中。我们就是通过在激活函数之前插入一个 BN 层,来解决这一问题。
Forward Pass
首先来看 Batch Normalization 的公式:

不难写出以下代码:
1 | sample_mean = np.mean(x, axis=0) |
其中,x 是 (N, D) 维度的数据,即本次 batch 有 N 条样本,每个样本的维度是 D。
为了方便在 test time 做 batch normalization,还要同时计算一个 running mean 和 running variance 当作估计值。
1 | running_mean = momentum * running_mean + (1 - momentum) * sample_mean |
Backward Pass
正向传播还算直观。接下来就要计算反向传播的梯度,以方便更新 gamma、beta 等参数。我们可以借助计算图,更容易地推导这几个要求解的导数:
$$
\frac{\partial out}{\partial x}, \frac{\partial out}{\partial \gamma}, \frac{\partial out}{\partial \beta}
$$
计算图如下:
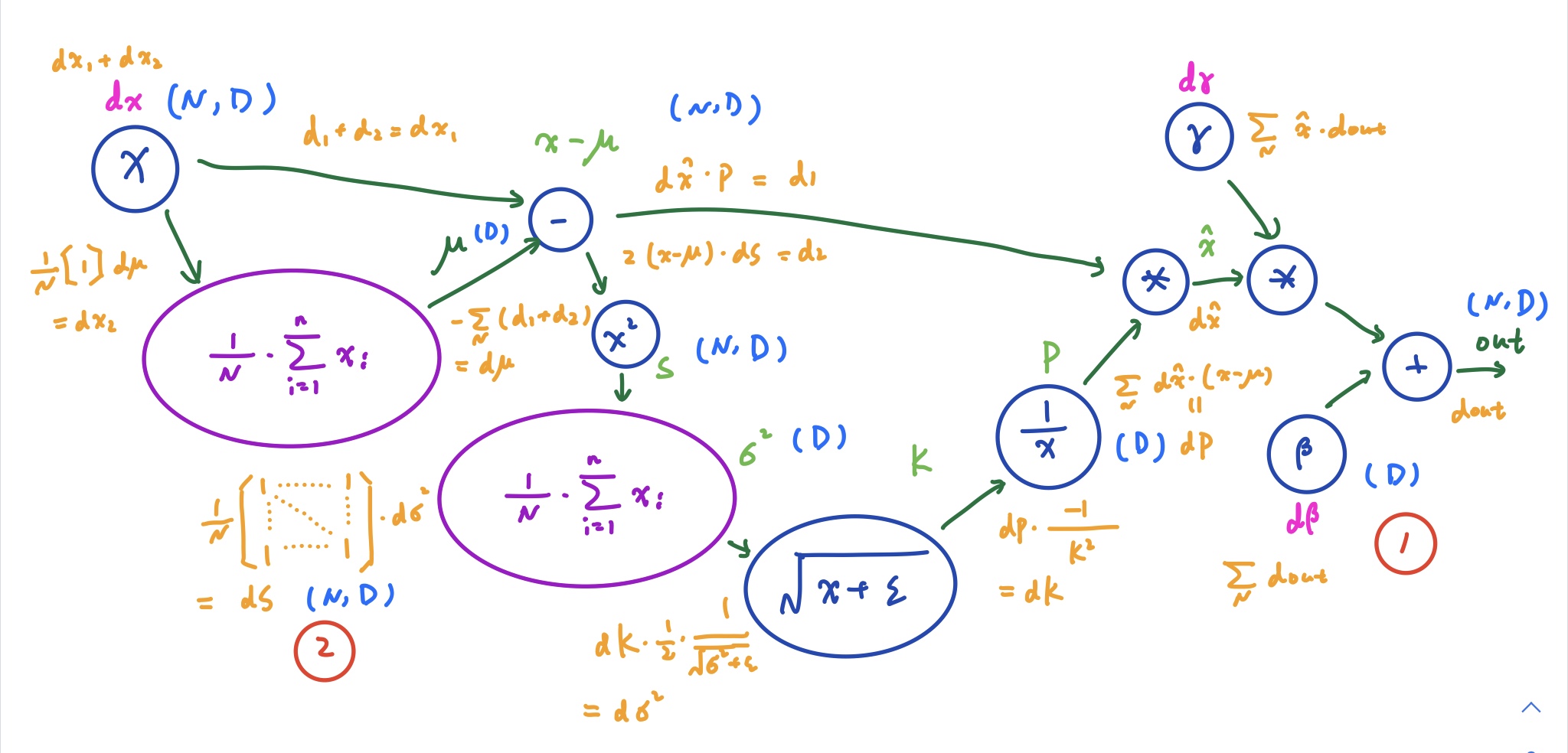
其中,浅绿色的文字代表正向传播的中间变量的值;橙色的文字代表反向传播的导数值;浅蓝色的文字代表了变量的维度。我们重点看其中的两个步骤。
红圈 1
这是我们反向计算的第一步。导数 dout 经过了一个加法运算。我们知道 x + y 对 x 或 y 求导,结果都是 1。根据链式法则,上一级的导数不会发生变化,也就是加法运算相当于导数的一个分配器 —— 导数被分流到两侧,而不发生变化。正常来说,d_beta 应该就等于 1 * d_out。但是如果我们看维度,就会发现 beta 本身的维度是(D),而 out 的维度是(N,D)。套用 numpy 中的概念来说,就是做加法的时候,beta 被 broadcast 了。也就是 beta 中某一个值对变化率(导数)的影响产生了 N 次。那在反向计算梯度时,就要把这 N 次累加起来。从 shape 来看,自然也就从(N,D)转化为(D)了。
红圈 2
这个步骤的导数计算就更加不直观了。但是本质上来说,这也是一个求和,因此导数也是会被派发给每个变量而不产生变化的。从这个角度思考,我们只需要将维度(D)的矩阵转化为维度(N,D)就可以了,因此构造一个维度为(N,D),元素全部为 1 的矩阵就可以了。从正向计算的角度思考,我们是通过求和的方式来让维度塌缩的,这和红圈 1 很类似。
通过计算图,我们也就可以确定哪些变量是可以在正向计算时缓存下来的了。
References
[1] 关于Batch_Normalization的公式推导和代码实现
[2] Understanding the backward pass through Batch Normalization Layer