直观理解 Wavelets
刚开始接触小波变换的时候完全搞不清楚其基本原理,对“多分辨率分析”、“时频分辨率”这些术语更是云里雾里。网络上好的教程极度稀缺。这时候就必须强烈推荐 The Wavelet Tutorial:http://users.rowan.edu/~polikar/WTtutorial.html ,真正做到了深入浅出,通读下来让人感觉受益匪浅。
Time Resolution
大家都很熟悉傅立叶变换(FT)了。FT 用无限长的正弦、余弦函数把时域信号变换到频域。但是它只告诉了我们信号中有哪些频率,没有告诉我们这些频率出现在哪里。从理论上说,这些频率每个时间点都有,毕竟从频域能完美还原出时域信号——但这不能满足工程的需要。
以下图来说,这个信号主要包含了 4 个频率分量。一开始频率较高,随后频率变低。如果我们将 0-300 ms 和 300-600 ms 的信号交换位置,他们的傅里叶变换会非常相似。毕竟信号的主要频率成分还是这些,并没有改变。当然严格来说,频率肯定是变了的,但是改变的部分都是次要的频率。在工程上我们肯定只关注主要部分,那么只看频谱图就会给我们一种信号相同的感觉。
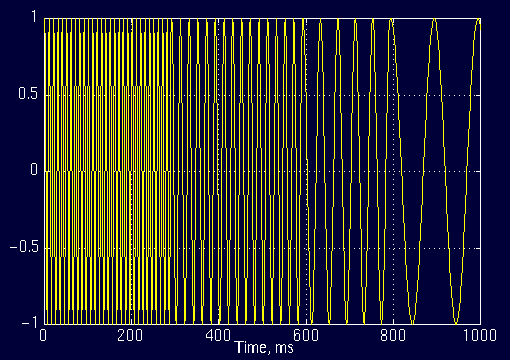
傅立叶变换没有时间分辨率!也就是说,它只适合用来分析平稳(stationary)信号,而现实中的信号往往都是非平稳信号。
Short Time Fourier Transform (STFT)
一个对傅立叶变换的直观改进就是短时傅里叶变换。既然信号不是平稳的,那么我们可以把它分割成很多小段,然后假定很小的时间片段内信号可以看成是平稳的。STFT 通过窗函数分割原始信号,并在窗口内进行傅里叶变换。公式如下:
$$
STFT_X^{(\omega)}(t,f) = \int_t \left[ x(t) \cdot \omega^*(t - t’) \right] \cdot e^{-j 2 \pi f t} dt
$$
可以看到,现在的 STFT 函数是和时间和频率都相关的了!也就是我们既可以知道有哪些频率,又可以知道这些频率出现在哪里。下图中有对称的两组峰,是因为傅里叶变换本身就具有对称性。
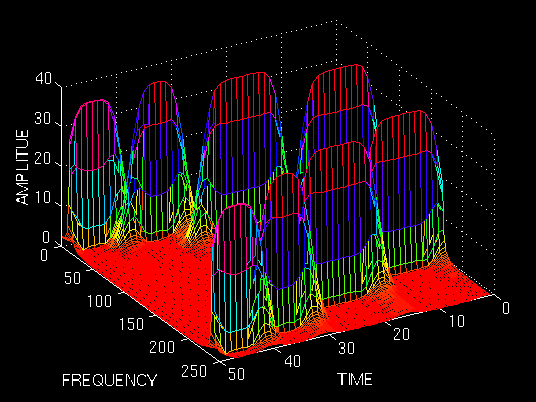
Heisenberg 测不准原理
测不准原理其实算是一种基本的自然法则,并不只局限于量子力学领域。在时频分析中,测不准原理是指时间分辨率和频率分辨率不能同时无限提高,而是存在互相制约的关系。提高时间分辨率,就会带来频率分辨率的下降,反之亦然。
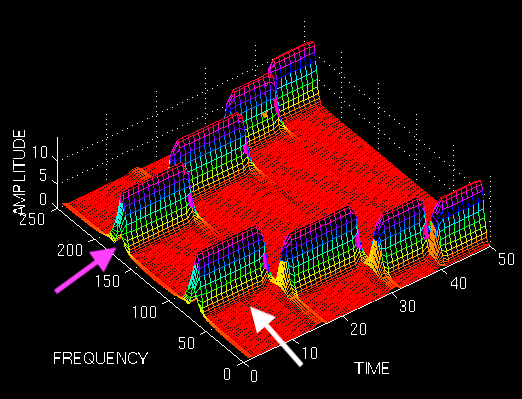
以 STFT 为例,如果我们用较窄的时间窗来做变换,自然提升了时间分辨率。毕竟窗口窄了,分析时间的精度就高了。以极限的角度思考,假如窗口无限长,那么就退化回普通的傅里叶变换了,自然完全谈不上时间分辨率了。下图可以看到,从时间轴看过去(白色箭头)边缘非常清晰;而从频率轴看过去(紫色箭头),就是类似高斯分布的形状,包含了很长一段频率区间。
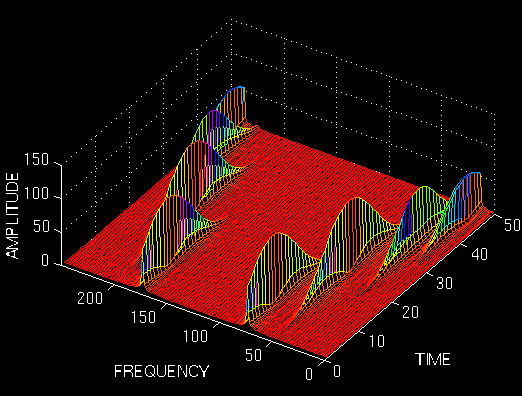
如果用较宽的窗口做变换,就正好相反。从频率轴的方向看,边缘非常锐利,几乎只有一个频率点有值。而时间轴上,很宽的范围内都有较大的值,甚至重叠在了一起。我们没有办法很好的分辨该频率具体出现在哪个时间点上。
Wavelet Transform
由于测不准现象的存在,我们很难去选择某一个长度的时间窗。小波变换通过多分辨率的方式来解决这一问题,公式如下:
$$
CWT_x^\psi(\tau,s) = \Psi_x^\psi(\tau,s) = \frac{1}{\sqrt{|s|}} \int x(t) \psi^* \left( \frac{t - \tau}{s} \right) dt
$$
小波变换首先需要一个母小波函数 $\psi$ ,它只在有限长的时间内有能量。小波变换与两个变量相关,即尺度 s 和位移 t,也就是把母小波压缩 / 拉伸,并且对每个尺度都平移扫描整个信号。我们知道时域上压缩信号,就相当于频域上的拓展,因此尺度 s 越小,对应的频率就越高。位移 t 自然反应了时间信息。小波变换的时频图如下:
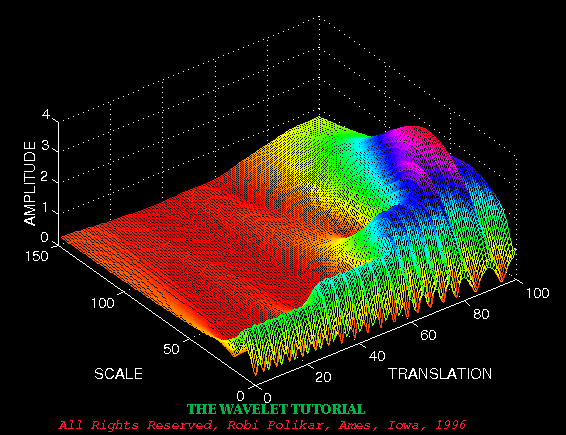
通过小波变换,我们在高频处获得了好的时间分辨率和差的频率分辨率。在低频处,我们获得了好的频率分辨率和差的时间分辨率。这很合理,因为高频往往代表着信号发生了突变,我们需要精确定位突变发生的时间。而低频分量往往分散在很广的时间范围内,因此不用对具体在哪里出现而特别关心。
Reference
The Wavelet Tutorial 写的非常好,非常感谢作者 Prof. Polikar 的付出:http://users.rowan.edu/~polikar/WTtutorial.html。然而其网站上所有 LaTeX 公式都没有渲染出来,读起来比较费劲。可以参考其 PDF 版本:https://web.iitd.ac.in/~sumeet/WaveletTutorial.pdf
一点小感想🤔
为什么互联网上大部分的资料 / 教程都很难懂呢?我想至少有以下三个原因:
- 他们不是写给普通人看的,也许搞数学的人就喜欢直接看公式,不用先建立一个感性的理解(By the math people, for the math people)。是我等凡夫俗子不能企及的高度,境界不够。
- 故弄玄虚,搞的高大上一些方能彰显作者水平。通俗易懂了岂不是显得很 low?
- 不懂装懂,自己也不理解自己写的啥,把别人写的东西无脑粘贴一下,毕竟天下文章一大抄。这点在某些中文博客平台很常见,四处“转载”,毫无原创。
希望能有更多像 The Wavelet Tutorial 一样的“说人话”的文章吧!