Bundle Adjustment using Ceres-Solver

Bundle Adjustment (BA) has a broad application in Structure From Motion (SFM) problems, which further optimize the location of points to achieve 3D reconstruction. In recent years, traditional filter-based SLAM algorithms have been taken place by optimization-based SLAM, in which BA is the core part. BA can simultaneously optimize camera poses as well as the locations of 3D points by minimizing the reprojection error.

Ceres-Solver is an optimization library that can be used to solve least-squares problems. There is an example program of solving BA on its official documents: http://ceres-solver.org/nnls_tutorial.html#bundle-adjustment

BAL Dataset

The example program uses Bundle Adjustment in the Large (BAL) dataset. This dataset uses a pinhole camera model, which has 9 parameters. There are 3 parameters for rotation R, 3 parameters for translation T, 1 parameter for focal length f, and two radial distortion parameters k1 and k2.

The data format in each file is described as follows:

• The first line includes 3 numbers, which are <num_cameras>, <num_points>, and <num_observations>.
• There are 4 numbers in each line of the following num_observations lines, representing <camera_id>, <point_id>, \, and \, respectively.
• The next 9 * <num_cameras> lines represents the camera parameters. Every 9 lines represent 1 camera. The order is the same with <camera_id>.
• The last 3 * <num_points> lines are the point locations. Every 3 lines represent 1 point. The order is the same with <point_id>.

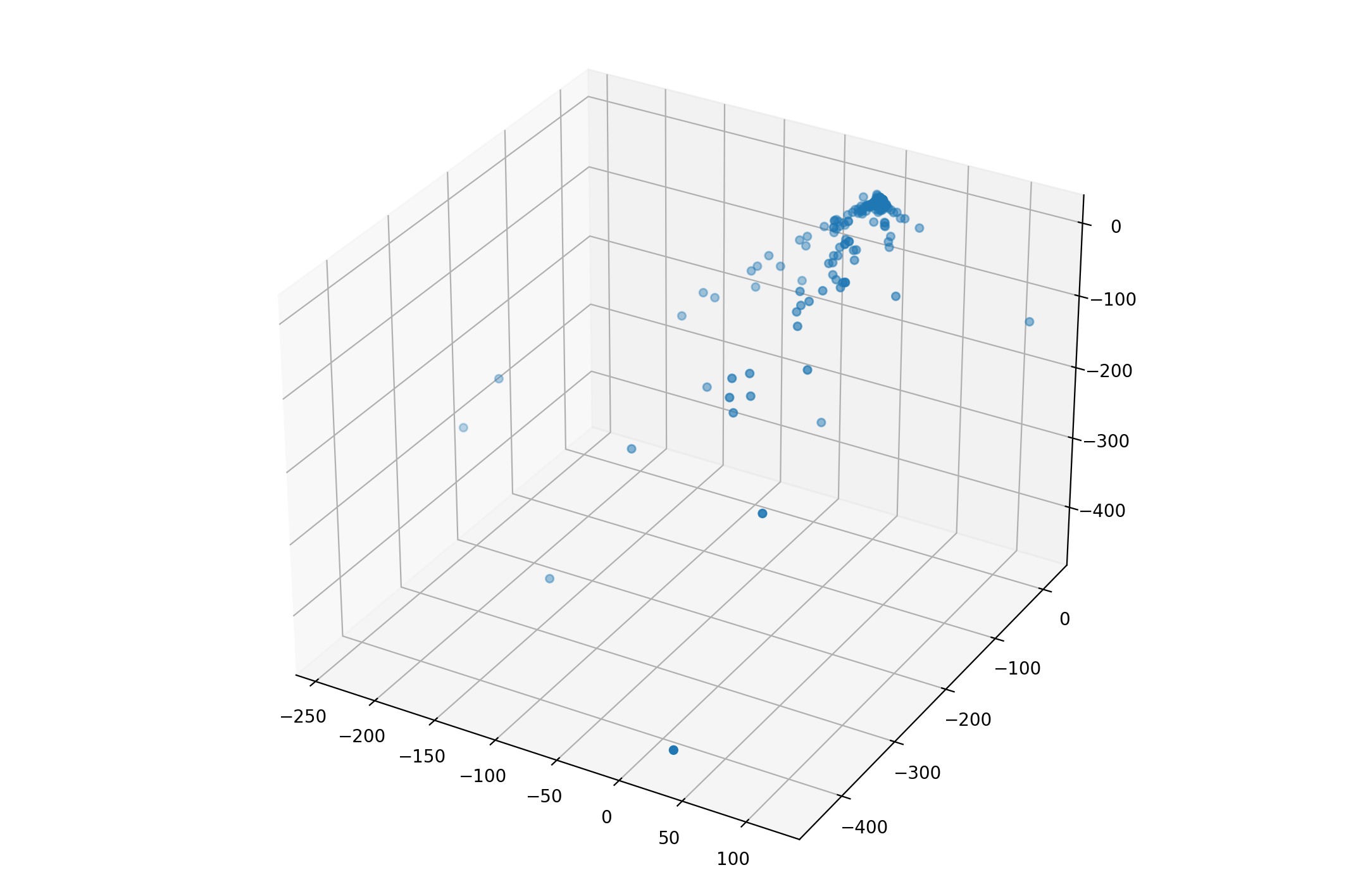
The following Python script can be used to visualize the points in a BAL data file. Here I took the first file in the LadyBug dataset as an example.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def read_bal_file():
    num_cam = 49
    num_points = 7776
    num_observations = 31843
    points = []
    with open('./ba_data.txt') as file:
        lines = file.readlines()
        for idx in range(1 + num_observations + 9 * num_cam, len(lines), 3):
            points.append([float(lines[idx].rstrip()), float(lines[idx + 1].rstrip()), float(lines[idx + 2].rstrip())])
    points = np.array(points)
    return points
    
def plot_3d(points):
    x_list = points[:, 0]
    y_list = points[:, 1]
    z_list = points[:, 2]

    fig = plt.figure()
    ax = Axes3D(fig)
    ax.scatter(x_list, y_list, z_list)
    plt.show()

points = read_bal_file()
plot_3d(points)

Compilation

The following CMakeLists.txt file can be used to build the program.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# cmake version to be used
cmake_minimum_required( VERSION 3.0 )

# project name
project(ba)

# target
add_executable( ba bundle_adjustment.cc )

# external libs
find_package(Ceres REQUIRED)
find_package(OpenCV REQUIRED)

target_include_directories(ba
  PRIVATE
    ${CERES_INCLUDE_DIRS}
    ${OpenCV_INCLUDE_DIRS}
)

target_link_libraries(ba 
  PRIVATE
    ${CERES_LIBRARIES}
    ${OpenCV_LIBRARIES}
)

Reprojection Error

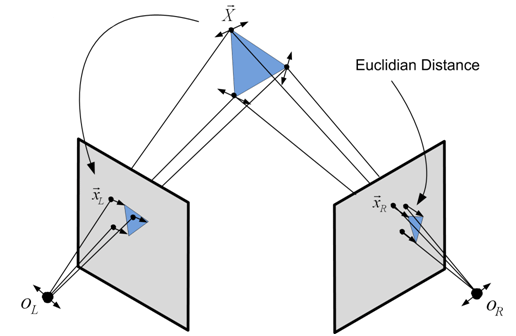
If we know the 3D coordinates of a point plus the intrinsic and extrinsic parameters of the camera, we can calculate the projection location of that point in the pixel frame. Ideally, the line from the optical center of the camera and the 3D point should overlap with this projection point. However, the measurement and the calculation are not perfect, there is an error in the projection. By optimizing camera parameters and the location of the 3D point, we can minimize the reprojection error, which is the idea of BA.

The cost function of BA is shown in the following formula:
$$
\frac{1}{2} \sum_i \sum_j | z_{ij} - h(T_i, p_j) |^2
$$
Where z is the measurement (point in the image plane) of point p at pose T. h is the measurement function, which converts the 3D coordinate of the given point into the 2D image frame. In the example program, we first convert the point from the world frame into the camera frame, using the extrinsic parameters (R and T). Then, undistortion is applied. Finally, we calculate the difference between the prediction with the observation and use it as the residual.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

struct SnavelyReprojectionError {
    SnavelyReprojectionError(double observed_x, double observed_y)
        : observed_x(observed_x), observed_y(observed_y) {}
    template <typename T>
    bool operator()(const T *const camera,
                    const T *const point,
                    T *residuals) const {
        // camera[0,1,2] are the angle-axis rotation.
        T p[3];
        ceres::AngleAxisRotatePoint(camera, point, p);
        // camera[3,4,5] are the translation.
        p[0] += camera[3];
        p[1] += camera[4];
        p[2] += camera[5];
        // Compute the center of distortion. The sign change comes from
        // the camera model that Noah Snavely's Bundler assumes, whereby
        // the camera coordinate system has a negative z axis.
        T xp = -p[0] / p[2];
        T yp = -p[1] / p[2];
        // Apply second and fourth order radial distortion.
        const T &l1 = camera[7];
        const T &l2 = camera[8];
        T r2 = xp * xp + yp * yp;
        T distortion = 1.0 + r2 * (l1 + l2 * r2);
        // Compute final projected point position.
        const T &focal = camera[6];
        T predicted_x = focal * distortion * xp;
        T predicted_y = focal * distortion * yp;
        // The error is the difference between the predicted and observed position.
        residuals[0] = predicted_x - observed_x;
        residuals[1] = predicted_y - observed_y;
        return true;
    }
    // Factory to hide the construction of the CostFunction object from
    // the client code.
    static ceres::CostFunction *Create(const double observed_x,
                                       const double observed_y) {
        return (new ceres::AutoDiffCostFunction<SnavelyReprojectionError, 2, 9, 3>(
            new SnavelyReprojectionError(observed_x, observed_y)));
    }
    double observed_x;
    double observed_y;
};

In the main function, the corresponding camera parameters and the 3D coordinates of each measurement are retrieved. All residual blocks are added into ceres::Problem and jointly optimized.

1
2
3
4
5
6
7
8
9
10
11
12

ceres::Problem problem;
for (int i = 0; i < bal_problem.num_observations(); ++i) {
    // Each Residual block takes a point and a camera as input and outputs a 2
    // dimensional residual. Internally, the cost function stores the observed
    // image location and compares the reprojection against the observation.
    ceres::CostFunction *cost_function = SnavelyReprojectionError::Create(
        observations[2 * i + 0], observations[2 * i + 1]);
    problem.AddResidualBlock(cost_function,
                             NULL /* squared loss */,
                             bal_problem.mutable_camera_for_observation(i),
                             bal_problem.mutable_point_for_observation(i));
}

Note that we can speed up the procedure of solving BA problems by utilizing its sparsity. However, it’s not demonstrated in this simple example.