Intro to Computer Graphics - Building 3D GitHub Contributions Graph

有这样一款插件，可以把 GitHub 的 contribution graph 用 3D 的形式展现出来，效果非常的炫酷。正好我最近正在看一些图形学的东西，干脆就自己实现一个可以动态旋转的 3D 图像来练练手。

想到放到 web 上来展示更便于分享，于是就使用了 WebGL + Three.js 框架。毕竟单纯使用 WebGL 操作还是太繁琐了，连 shader 都要自己写。

效果

效果如下，还是比较好看的：

也可以访问 www.luyuan.wang 点击最下方的 statistics 按钮来查看。美中不足就是因为工作比较忙，这一年来都没什么时间写自己的代码，contributions graph 比较稀疏😂。

图形学概述

如果知道物体的信息，怎么把图像画到屏幕上去呢？我们都知道屏幕是有像素阵列组成的，通过扫描的方式依次去给每个像素设置不同的 RGB 值。屏幕是一个光栅设备，绘制的这一过程就称为光栅化（Rasterization）。

那么已知物体的信息，怎么直到该点亮屏幕上的哪些像素点呢？这就要使用所谓的 MVP 变换。MVP 是 Model - View - Projection 的简写。通俗来说，Model 是指找来模型（物体），View 是把摄像机的位置摆放好，Projection 就是拍照。在图形学中，我们习惯把摄像机放在原点的位置，以 y 轴为正上方方向（up at y axis），并看向 -z 的方向（look at -z axis）。

View / Camera Transformation

现实中，物体是随意摆放的，相机也是随意摆放的。为了把相机挪动我们习惯的原点，而拍摄到的相片内容不变，就要把所有的物体跟着一起转动过去。所谓“山不来就我，我就山”。

假设相机原始的位置是 e ，look at g, up to t。首先我们需要移动 e 到原点的位置，然后再旋转 g to -z ，t to y 。当然，第三个轴自然也就跟着转动过去了（右手系）。

经过推导，可得：

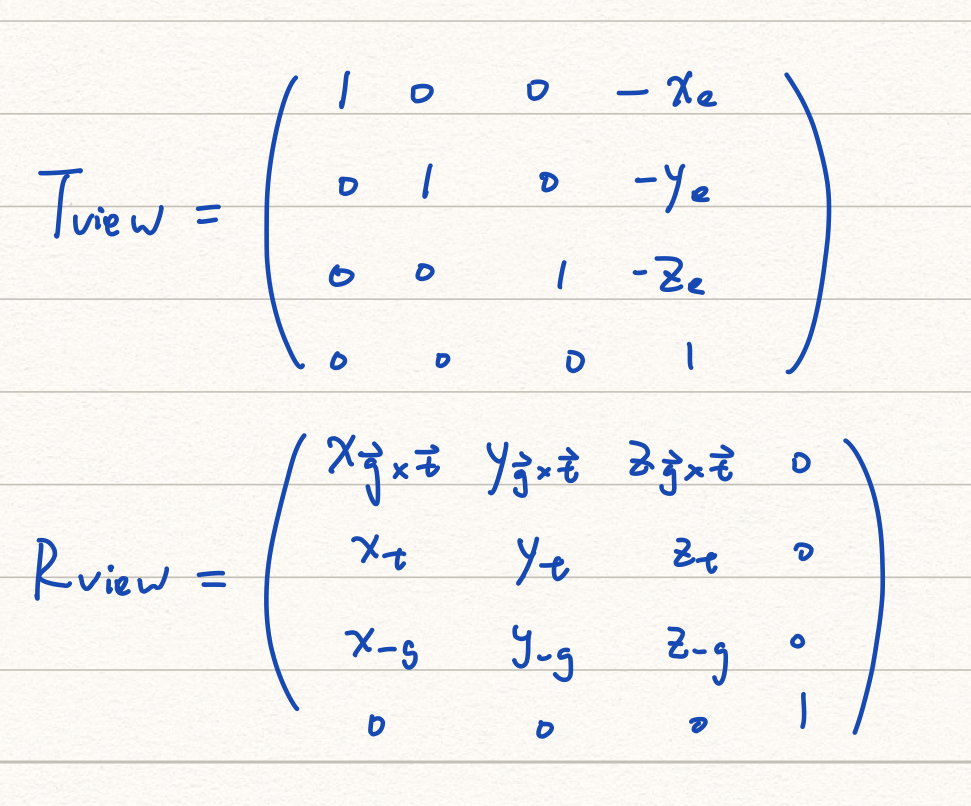
而最终的变换矩阵则为：
$$
M_{view} = R_{view}\cdot T_{view}
$$
那我们为什么要做这样的变换呢？答案是为了更方便做下一步：投影。

Projection Transformation

有两种投影方式，正交投影和透视投影。正交投影中，原本平行的线经过投影后仍然平行。透视投影则是我们日常肉眼见到的样子，所谓近大远小。两个平行的铁轨不再平行，而是相交于远处的一点🛤️。当我们把相机拉到无穷远处，也就没有了所谓的近大远小（远近的概念失去意义），这个时候看到的画面就是正交投影了。

正交投影的矩阵为：

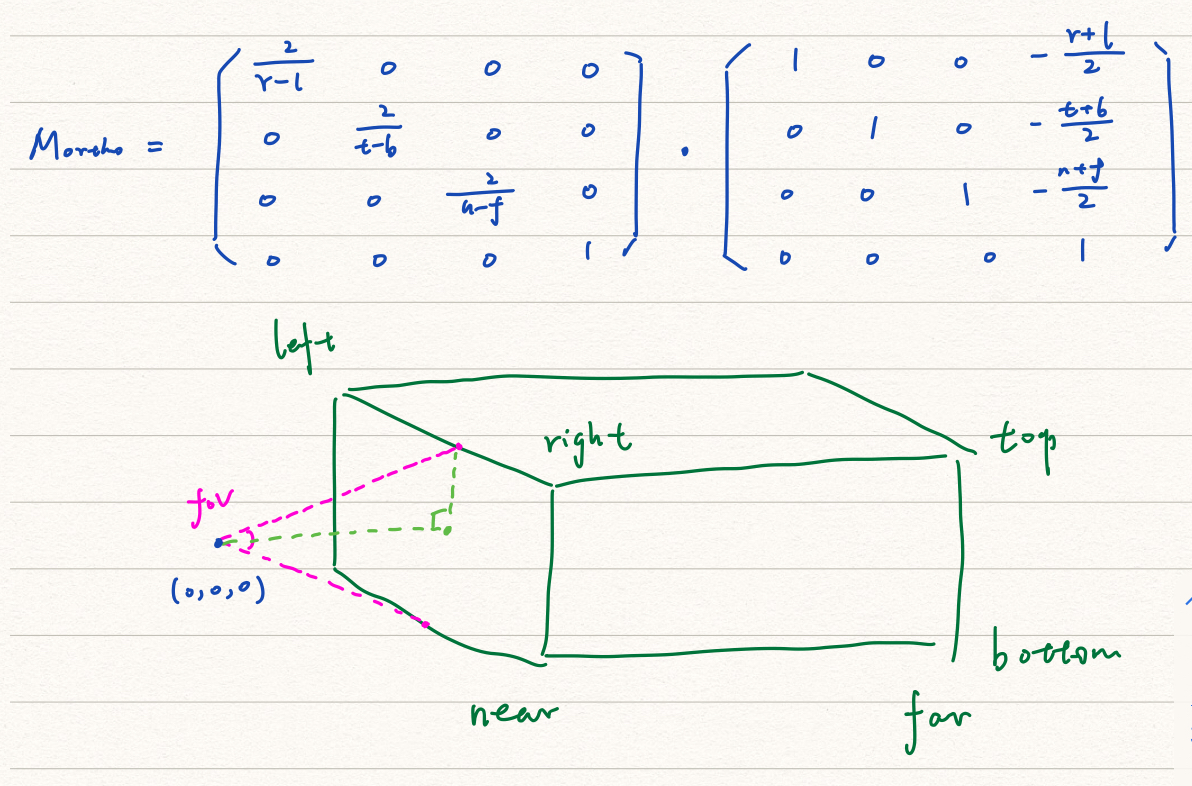
透视投影可以分成两步，首先先把空间进行挤压，然后再做正交投影。

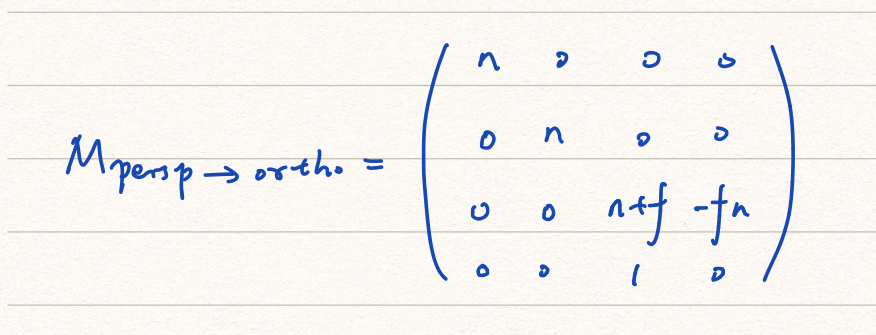
最终的透视投影矩阵为：
$$
M_{persp}=M_{ortho}\cdot M_{persp\rightarrow ortho}
$$

Viewport Transformation

投影矩阵会把世界压缩到 [-1, 1] ^ 3 的立方体里。我们还需要根据屏幕大小，把它变换到屏幕的尺寸上。这一步就称为视口变换。

光栅化

我们平时在说图像性能时，经常会说“每秒能渲染多少个三角形”。三角形在图形学里非常重要，这有以下几个原因：

• 三角形的表现力很强，用三角形可以近似表示出非常复杂的曲面。
• 三个顶点构成的三角形一定在一个平面上
• 三角形的内部、外部很好区分（有很简单的算法）
• 三角形内部有 well-defined 的插值算法

通过刚刚的变换，物体（很多很多个三角形）已经变换到屏幕空间了。那么该怎么决定点亮哪些像素呢？要知道物体时连续的，而像素时离散的。答案很简单，通过用像素中心点的位置进行采样就可以了。

好的，现在我们已经能在屏幕上绘制出物体了。

着色 Shading

单纯的画出物体，只能看到一些色块，显得不够真实。这个时候就需要对它们进行着色，比如，在不同的光线下，物体的颜色会发生变化。

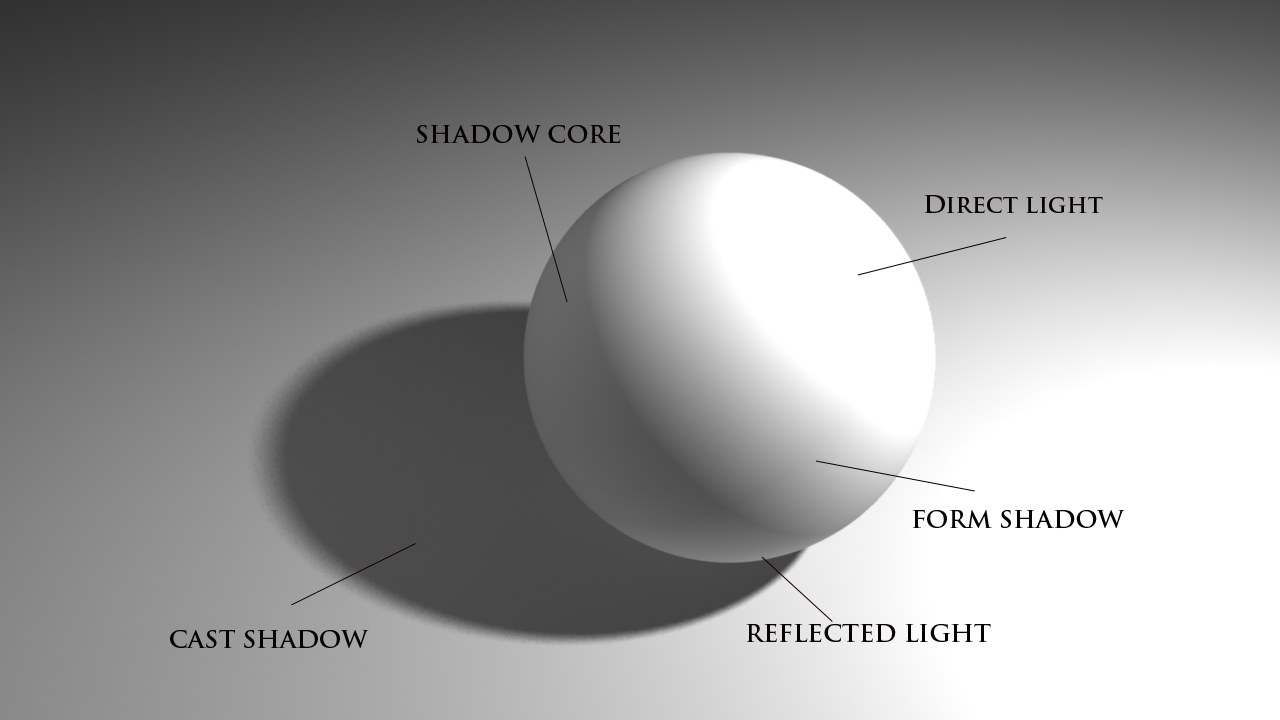
一种简单的 shading model 是 Blinn-Phong 反射模型。他简化了光线的传播规律，把我们看到的反射光分为三项：高光、漫反射、环境光。通过对这三项进行叠加，可以给出一个不错的效果。

图中最左侧就是 Phong 的效果，Blinn-Phong 是 Phong 的一种改进算法。是不是比右侧没有 shading 的球看起来真实许多呢？当然，Phong 模型到底也是一个简单的模型，虽然能给出不错的效果，但离可以欺骗肉眼还有一定的差距。要想达到非常逼真的效果，简单的光栅化就不够了，就需要用到光线追踪技术。

现代的显卡都具有编程能力，可以通过 GLSL 语言来编写自定义的 Shader 程序。

Texture

贴图的原理很简单，就是给一张图片，上面带有三角形顶点的映射关系。这样我们就可以根据三角形的顶点，把图片给“贴”到对应的模型的顶点处。这个映射关系是由设计师在设计贴图时编辑进去的，可以认为是已知量。

实现思路

上面简要介绍了计算机图形学最基本的一些原理。那么这个 3D 的 contributions graph 到底是怎么画出来的呢？其实很简单，只需要根据贡献的次数来绘制一些高度不同的长方体、打上光照、再进行旋转就可以了。至于原始的数据，可以考虑直接爬取 GitHub 网站，调用 API 拼凑反而显得困难了。

实现细节

首先，我们来定义相机的参数：

1
2
3
4
5
6

const fov = 75;
const aspect = 2;  // the canvas default
const near = 10;
const far = 1000;

const camera = new THREE.PerspectiveCamera(fov, aspect, near, far);

在介绍 Projection Matrix 的地方有一张图，可以看到 fov 是相机视线的夹角大小。Aspect 是画面的长宽比，这里暂时设定一个默认值，实际应该根据 canvas 的长宽比设置。

1
2
3
4

camera.position.x = 0;
camera.position.y = -400;
camera.position.z = 200;
camera.lookAt(new THREE.Vector3(0, 0, 0));

接下来我们设置了相机的位置，可见 x 轴是原点处，y 轴向后退了一些，z 轴向上升高了一部分。接下来旋转相机，让它看向原点的方向。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

for (var week = 0; week < 53; week++) {
    for (var day = 0; day < 7; day++) {
        //......
        let geometry = new THREE.BoxGeometry(9.5, 9.5, depth);
        let material = new THREE.MeshPhongMaterial({ color: color });
        let cube = new THREE.Mesh(geometry, material);

        cube.position.x = currentX;
        cube.position.y = currentY;
        cube.position.z = (depth / 2);
      
        scene.add(cube);
      	//......
    }
}

接下来依次绘制长方体。首先要构造一个几何形体 geometry，就是一个 box。长款都一样，高度由 contribution 次数决定。然后要构造材质，为了有一个真实的光照效果，使用了 Phong 材质。几何形体 + 材质，就构成了一个网格 mesh。我们可以想象，这样的一个立方体是由 6 个面组成的，每个面是一个长方形，可以由 2 个三角形拼接形成。那么一个立方体就需要 12 个三角形。

绘制顶部的说明文字就比较 tricky，因为 three.js 并没有提供特别直观的 2D 文字 API。这里的思路是绘制一个 2D 的长方形表面，然后贴一个纹理上去。纹理贴图的内容就是文字。这是利用了 three.js 支持 canvas 作为贴图的特性。

1
2
3
4
5
6
7
8
9
10
11

// draw text picutre
var canvas = document.createElement('canvas');
context.fillText(text, x, y);
// generate texture with that picture
var texture = new THREE.Texture(canvas);
texture.needsUpdate = true;
const geometry = new THREE.PlaneBufferGeometry(250, 100);
// apply texture
const material = new THREE.MeshBasicMaterial({ map: texture, side: THREE.DoubleSide });
material.transparent = true;
const mesh = new THREE.Mesh(geometry, material);

这里只需要把材质本身设置成透明的，就看不出来 canvas 上没有文字的部分啦！

结束语

至此，一个 3D 的 GitHub contributions 图就画完了。虽然非常简单，但也算是利用图形学的知识的一次小小的实战，还是挺有意思的。