What is Gumbel Softmax?
看了几篇博客,都对 Gumbel Softmax 讲解的不是很到位。这里重新总结了一下,希望从“要解决什么问题”的角度把这个 trick 梳理清楚。
随机模型的困难:采样
我们常见的深度学习模型是确定的(deterministic)模型,比如一个用于区分猫和狗的 CNN 网络。当网络的参数固定时,同样的输入总是会有同样的输出。然而还有一些场景是需要随机的(stochastic)模型的。这样的模型是有不确定性的,即同样的输入、同样的参数,也会有不一样的输出。
比如在强化学习中训练一个游戏 AI。这个 AI 应当是以一定的概率往前后左右四个方向行走的。假如经过计算,四个方向运动的概率分别是(0.9, 0.05, 0.05, 0.0),那么 AI 不应该永远朝着概率最大的第一个方向运动。在训练过程中,它也应该有 0.05 的概率真的走向第二个方向。又比如在 Learning in the Frequency Domain 论文中,频率通道的动态选择是有一定概率的。即 10 次中可能有 8 次选择了 A 通道,而不是说当概率 > 0.5 时就永远选择 A 通道。
也就是说,我们的模型在训练过程中需要以一定的概率分布进行采样。即给定一个概率分布函数,需要有一个算法来产生各种各样的样本值。一个简单但常用的采样算法是拒绝采样(reject sampling)。
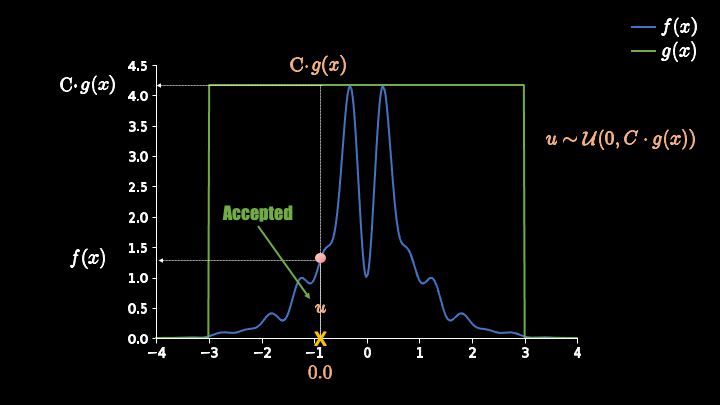
途中,蓝色的线代表了一个我们的目标概率分布函数。这个函数很复杂,因此我们用一个简单的均匀分布(绿色)来把它包围起来。这个时候我们先随机选一个样本点(黄色 x),然后再产生一个随机数 u。当 u 的值落在蓝线下方时,我们接受这个样本点;反之则拒绝。这样被我们接受的样本点就符合目标概率分布了。
刚刚提到产生一个随机数 —— 也就是要对均匀分布进行采样。均匀分布的采样可以通过“线性同余发生器”来实现。这是一种伪随机数发生器。
听起来比较简单,但是在深度学习中,这会带来一个严重的问题:采样的过程显然是不可导的!我们的神经网络没有办法通过反向传播来更新参数了。
Re-parameterization
解决采样问题不可导的一个 trick 是重参数化:re-parameterization。以高斯分布为例,假如我们需要对一个 N(mu, sigma) 采样,我们可以把它转化成对 N(0, 1) 采样,然后再缩放。这样就相当于改变了采样的先后顺序,把真正的采样过程移到计算图的边缘,就不影响对参数 mu、sigma 和 x 的导数计算了。
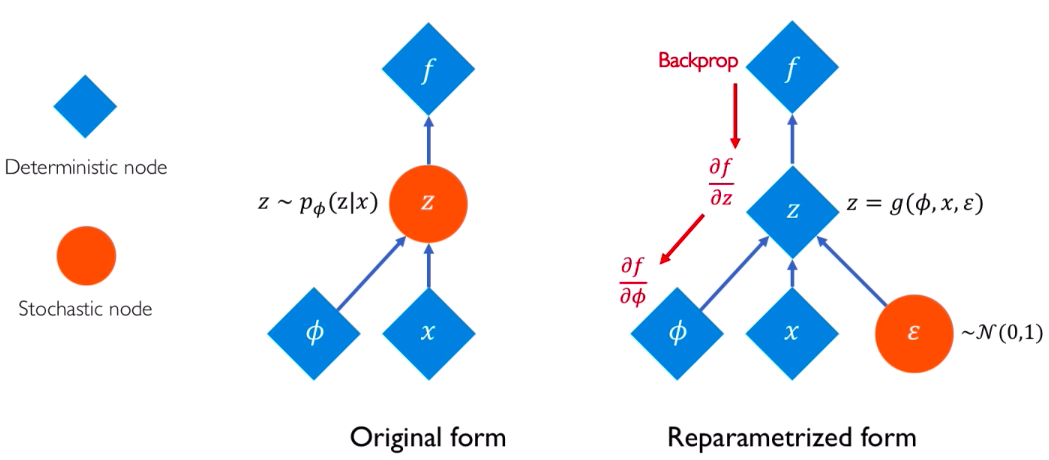
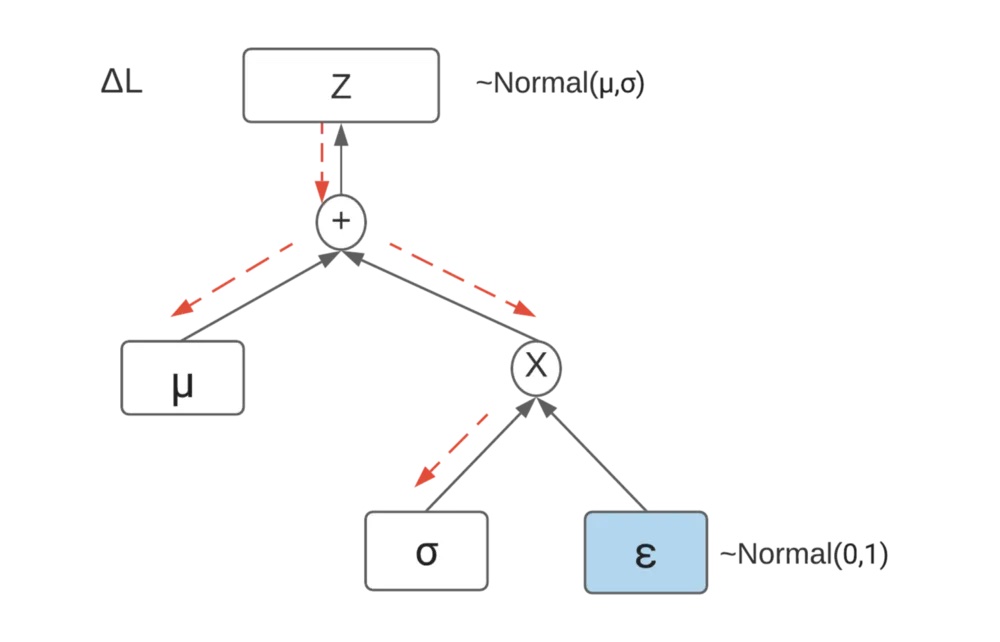
对于反向传播来说,只把采样产生的样本值当成一个确定的常数就可以了。这个 trick 典型的应用例子是 VAE。
Gumbel Max Trick
在 Learning in the Frequency Domain 中,动态的通道选择就需要从伯努利过程中采样。针对离散的情况,我们同样需要利用 re-parameterization 来计算导数,就像在上述的连续情形中一样。
我们可以用 Gumbel Max 的方式来实现采样:
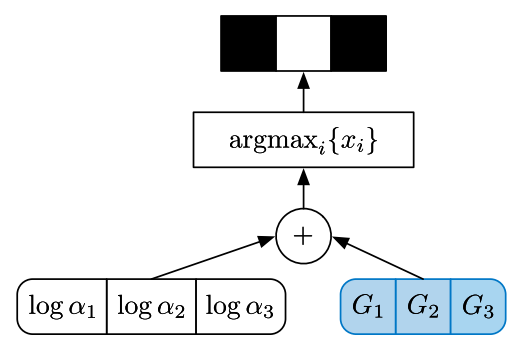
假设我们有三个事件的概率,分别为 a1,a2 和 a3。我们希望采样后的输出是一个 one-hot 的编码,例如 [0, 1, 0],或者 [0, 0, 1]。当然这个输出是要符合 (a1, a2, a3) 的概率分布的。我们引入 Gumbel noise,让噪声和 log(a) 相加,之后做 argmax 得到 one-hot 编码。这个过程和上一节的高斯分布的做法一致,都是把采样的操作放到了计算图的边缘节点,这样就不影响其他分支的导数计算。
计算公式如下:
$$
z = OneHot(\mathop{argmax}\limits_{i}[g_i + log\alpha_i])
$$
Gumbel Noise
什么是 Gumbel Noise 呢?Gumbel 分布是一种极值分布。假如说每天测量 100 次心率(假设心率服从正态分布),记录最大的心率。多次观察,那么这个最大的心率就服从 Gumbel 分布。
服从 Gumbel 分布的随机变量可以通过以下公式计算:
$$
G_i = -log(-log(\epsilon_i))
$$
$$
\epsilon_i \sim Uniform(0, 1)
$$
为什么选择选择 Gumbel Noise 呢?数学上可以证明对每个值加上一个独立标准 Gumbel 噪声后,取最大值,得到的概率密度和 softmax 一致。通过实验,也可以验证如果使用其他的噪声,概率会失真。具体的实验结果和数学证明可以参考这篇文章,证明过程还比较复杂。
Gumbel Softmax
上述的 Gumbel Max Trick 以 re-parameterization 的方式解决了采样不可导的问题。但是它又新引入了一个 argmax 的操作,而 argmax 同样是不可导的。解决办法是引入 softmax,来模拟 argmax 运算。
$$
y_i = \frac{exp(x_k / \tau)}{\Sigma_{i=1}^nexp(x_i / \tau)}
$$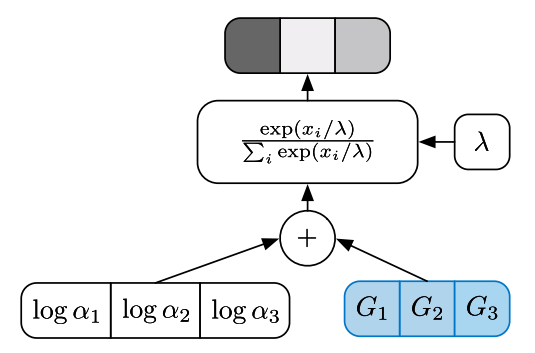
这里的 $\tau$ 代表温度,是一个超参数。它用来控制随机性,就像物理学中,温度越高,例子的运动越剧烈,随机性越大一样。
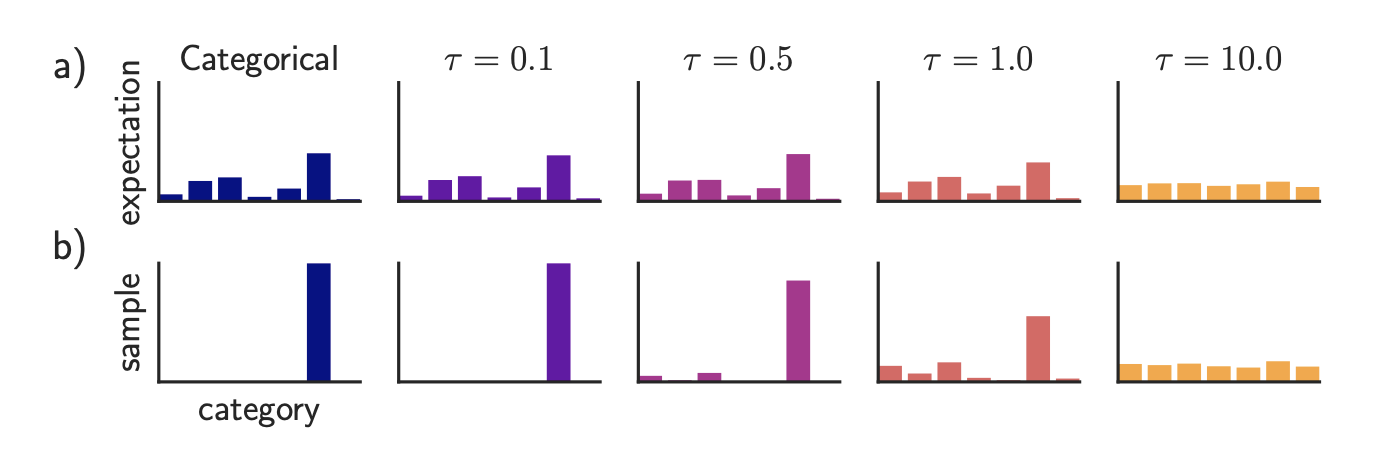
当温度较小时,就非常接近 argmax。当温度较大,也就更接近于均匀分布。
总结
- 某些情况下我们需要引入随机性,比如动态通道选择中,通道要以一定的概率被选择 / 不选择。而采样过程不可导,无法应用反向传播。
- 通过 Gumbel Max Trick 这一 re-paramerization 的方式,我们可以绕过采样的步骤。但是又引入了新的不可导运算 argmax。
- 通过 Gumbel Softmax 可以模拟 argmax 运算,从而解决了导数计算的问题。